¿Cómo calcular el coeficiente de variación en Excel? - Aprende a hacer el cálculo

En el mundo del análisis de datos y la estadística, es fundamental comprender la variabilidad de un conjunto de datos. Una de las herramientas más poderosas para medir esta variabilidad es el coeficiente de variación. Desde esta perspectiva, te mostraremos cómo calcular el coeficiente de variación en Excel explorando su importancia, interpretación y utilidad.

¿Qué es el coeficiente de variación?

El coeficiente de variación es una medida estadística utilizada para evaluar la variabilidad relativa de un conjunto de datos. Expresa el grado de variación en relación con la media aritmética (promedio) de los datos. En esencia, el CV (coeficiente de variación) permite comparar la dispersión de los datos entre conjuntos de datos con diferentes unidades o escalas.

Matemáticamente, el coeficiente de variación se calcula como:

CV = (desviación estándar / media) x 100

Donde, 'Desviación estándar' representa la medida de la dispersión de los datos y la 'Media' es el promedio del conjunto de datos. El resultado del cálculo del coeficiente de variación suele expresarse en porcentaje.

Importancia del coeficiente de variación

Dada su capacidad para proporcionar información valiosa sobre la variabilidad de los datos, el coeficiente de variación desempeña un papel fundamental en el análisis estadístico. Comprender su significado es esencial para tomar decisiones eficaces en diversos campos. Los siguientes son algunos ejemplos que muestran su importancia:

• Normalización: el CV permite comparar conjuntos de datos con diferentes unidades o escalas. Esto facilita la extracción de conclusiones significativas incluso cuando se trata de datos de magnitudes variables.
• Evaluación de riesgos: en finanzas e inversión, el CV es una herramienta fundamental para evaluar el riesgo. Un CV más alto sugiere una mayor variabilidad y, por tanto, un mayor riesgo, lo que ayuda a los inversores a tomar decisiones sustentadas.
• Control de calidad: las industrias se basan en el CV para controlar la calidad de los productos. Un CV bajo indica procesos de fabricación consistentes, mientras que un CV alto puede indicar problemas que requieren atención.

Cálculo del coeficiente de variación en Excel

Microsoft Excel es una herramienta versátil para realizar diversos cálculos estadísticos, incluido el coeficiente de variación, para el cual puedes usar plantillas. En este contexto, te mostramos el proceso paso a paso para calcular el coeficiente de variación en Excel. Para ello, utilizamos como ejemplo un conjunto de datos relacionados con los rendimientos mensuales de dos carteras de inversión diferentes a lo largo de un año.

Preparar tus datos

Antes de poder calcular el coeficiente de variación, es fundamental tener los datos correctamente organizados en una hoja de cálculo de Excel. Sigue estos pasos para hacerlo:

• Estructura de datos: asegúrate de que los datos están organizados en una estructura clara y lógica. Coloca el conjunto de datos en una sola columna o fila.

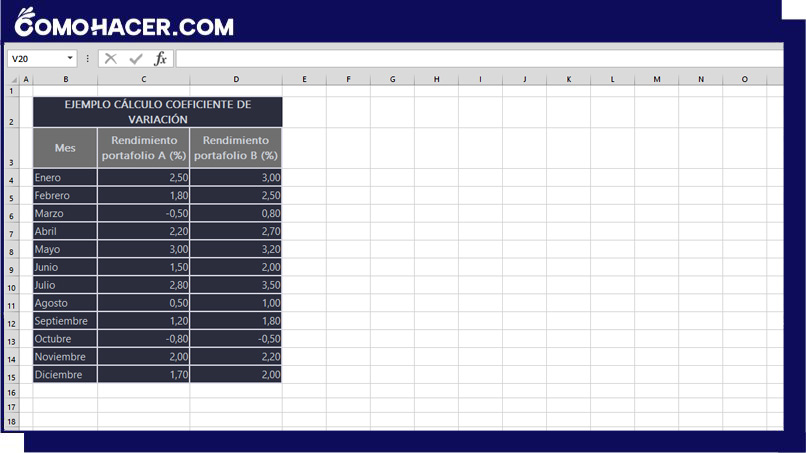
• Rango de datos: determina el rango de celdas que contienen los datos.
• Validación de datos: antes de continuar, valida los datos para detectar errores, valores omitidos o valores atípicos. Resuelve cualquier problema para asegurar la integridad de su análisis.

Calcular la media y la desviación estándar

El siguiente paso para calcular el coeficiente de variación es calcular la media (promedio) y la desviación estándar de tu conjunto de datos. Te explicamos cómo hacerlo:

Calcular la media

Selecciona una celda vacía en la que desees mostrar la media. Utiliza la fórmula =PROMEDIO(rango), sustituyendo 'rango' por el rango de celdas de sus datos (por ejemplo, =PROMEDIO(C4:C15)).

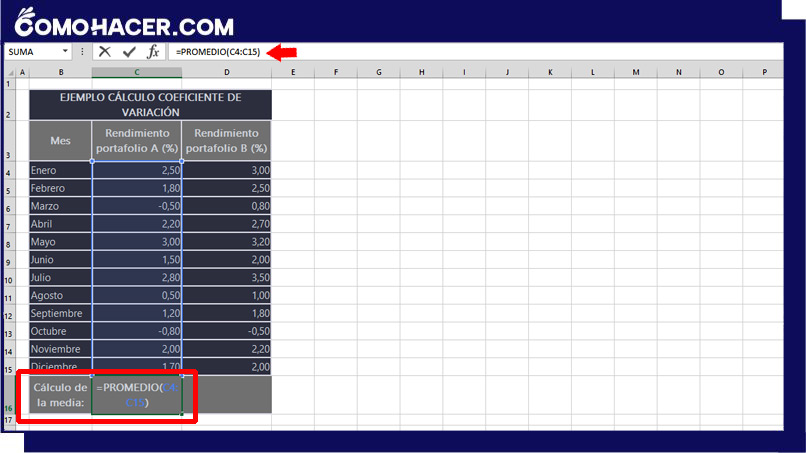
Al aceptar la fórmula introducida, Excel muestra el resultado en la celda seleccionada. Para hacer el cálculo de la media de la “cartera B” copia la fórmula en la celda que selecciones.

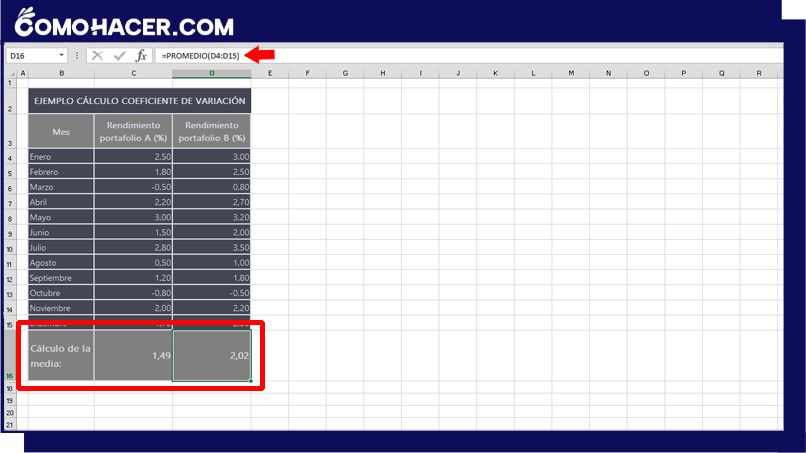
Calcular la desviación típica

Del mismo modo, selecciona otra celda vacía en la que desees mostrar la desviación estándar. Utiliza la fórmula = =DESVEST.M (rango), donde 'rango' representa el rango de celdas de tus datos (por ejemplo, =DESVEST.M(C4:C15)).

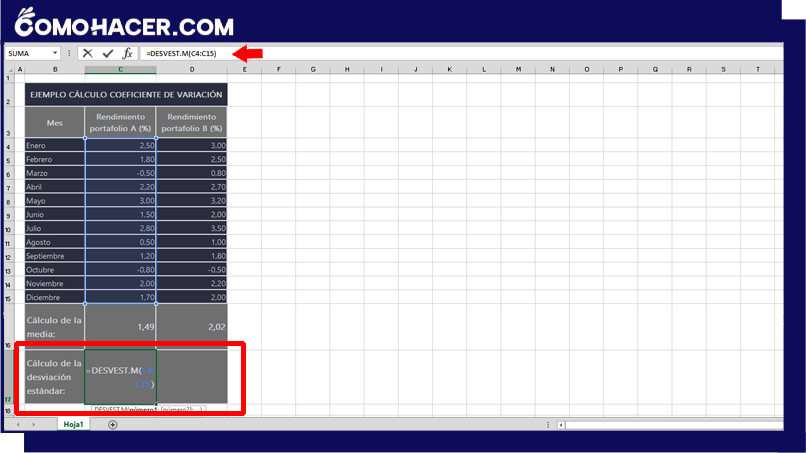
Al aceptar la fórmula introducida, Excel muestra el resultado en la celda seleccionada. Para hacer el cálculo de la desviación estándar de la “cartera B” copia la fórmula en la celda que selecciones.

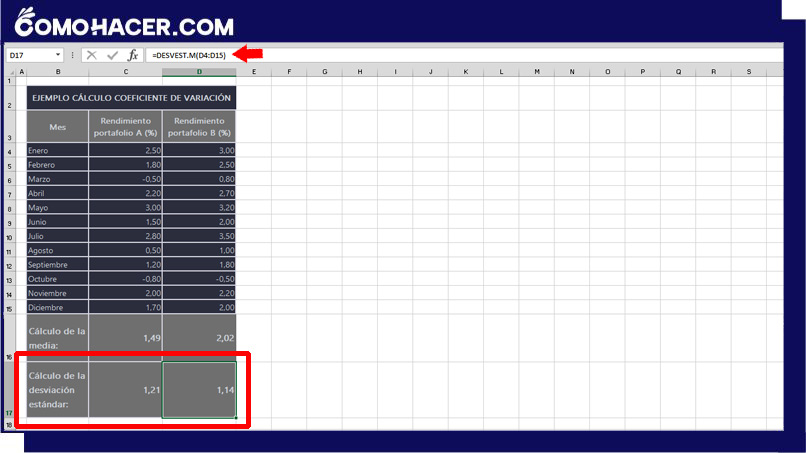
Ahora ya dispones de la media y la desviación típica de tu conjunto de datos para su posterior análisis.

Calcular el coeficiente de variación

Una vez obtenidas la media y la desviación típica, puedes calcular el coeficiente de variación en Excel. A tal efecto, elige una celda vacía donde quieras mostrar el coeficiente de variación.

Utiliza la fórmula =(DESVEST.M (rango) / PROMEDIO (rango)) * 100. Esta fórmula calcula el coeficiente de variación como porcentaje. Por ejemplo: =(DESVEST.M (C4:C15) / PROMEDIO (C4:C15))*100.

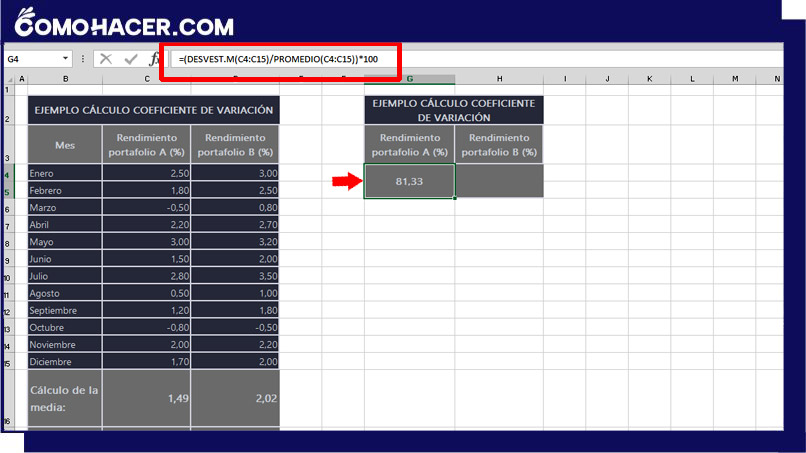
Opcionalmente, puedes simplificar el proceso utilizando los resultados ya obtenidos. Usando el ejemplo, sería de este modo: =C17/C16 * 100.

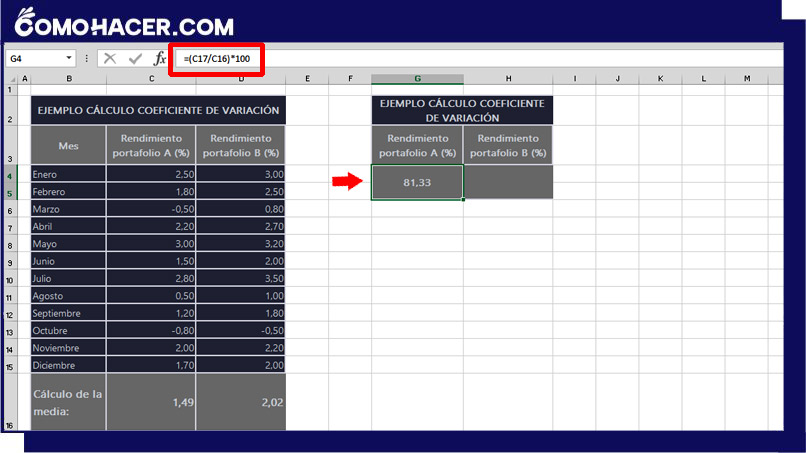
Una vez que introduzcas esta fórmula, Excel realizará el cálculo y presentará el coeficiente de variación para tu conjunto de datos. Para hacer el cálculo de la desviación estándar de la “cartera B” copia la fórmula en la celda que selecciones.

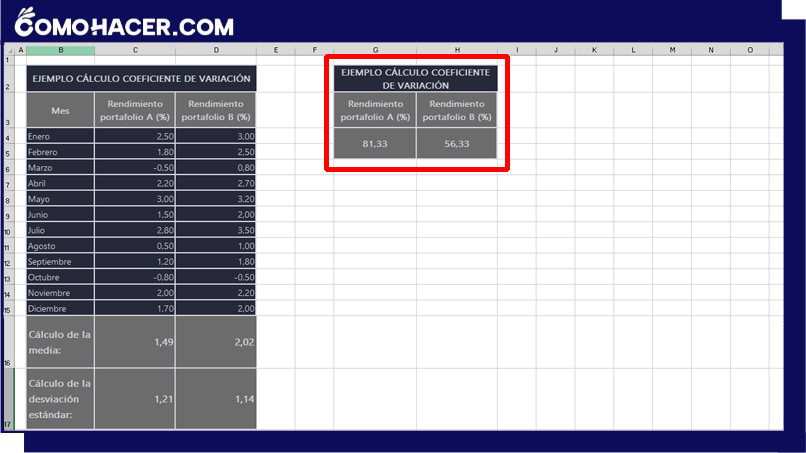
Interpretación y utilidad del coeficiente de variación

Comprender el coeficiente de variación calculado es esencial para tomar decisiones con conocimiento de causa. A continuación te explicamos cómo interpretarlo y utilizarlo:

Coeficiente de variación bajo y alto

Los valores bajos y altos del coeficiente de variación son métricas esenciales para un análisis eficaz de los datos.

• CV bajo (inferior al 15%): Un CV bajo sugiere que los puntos de datos están estrechamente agrupados en torno a la media. Esto indica un conjunto de datos relativamente estable. En términos financieros, las inversiones con un CV bajo se consideran más seguras, ya que muestran un rendimiento constante.
• CV moderado (15 a 35%): este rango indica un nivel moderado de variabilidad en comparación con la media. El CV moderado es típico en varios escenarios del mundo real, lo que significa una mezcla equilibrada de estabilidad y variación.
• CV alto (superior al 35%): sugiere una variabilidad significativa en relación con la media. Esto indica un conjunto de datos menos estable con respecto a la media. En finanzas, las inversiones con un CV alto se consideran más arriesgadas debido a su rendimiento impredecible.

Comparación de conjuntos de datos

Evaluar el coeficiente de variación (CV) entre diferentes conjuntos de datos es crucial para tomar decisiones informadas y evaluar el riesgo. Para comparar conjuntos de datos con eficacia:

• Considera el contexto: evalúa cómo se ajusta el CV a los objetivos específicos del análisis y a la naturaleza de los datos.
• Evaluación del riesgo: si la estabilidad y la reducción del riesgo son tus objetivos principales, favorece las inversiones o los activos con un CV más bajo.
• Identificar valores atípicos: ten cuidado con los valores atípicos que pueden sesgar los resultados del CV.
• Tamaño de la muestra: reconoce que la fiabilidad del CV aumenta con tamaños de muestra mayores, lo que lo hace más adecuado para analizar conjuntos de datos extensos.

Consejos para un cálculo preciso del coeficiente de variación en Excel

Estos son algunos consejos adicionales para asegurar la precisión del cálculo del coeficiente de variación en Excel:

• Valida los datos: comprueba la exactitud del conjunto de datos y asegúrate de que no hay errores o valores atípicos que puedan sesgar los resultados.
• Datos robustos: para conjuntos de datos más pequeños, ten cuidado ya que el coeficiente de variación puede no ser tan fiable. Generalmente es más robusto para conjuntos de datos más grandes.
• Unidades coherentes: asegúrate de que las unidades de medida del conjunto de datos son coherentes para obtener resultados significativos.
• Formato: formatea la celda del resultado del coeficiente de variación como un porcentaje para una mejor legibilidad.